In geometry, cone is a solid or hollow object with a round flat base and sides that slope up to a top point. The cone formulas, solved example & step by step calculations may useful for users to understand how the input values are being used in such calculations. Also this featured cone calculator uses the various conversion functions to find its area, volume & slant height in SI or metric or US customary units. Calculate the unknown defining side lengths, circumferences, volumes or radii of a various geometric shapes with any 2 known variables. Online calculators and formulas for a surface area and other geometry problems. A cone is a 3D shape with only one vertex, having a circular base.
The top most point of a cone is the vertex or apex. The slant height of a cone is defined as the distance from the apex to any point lying on the circumference of the base. The slant height is usually denoted by letter 'l' or even sometimes by the letter 's'.
In the right circular cone calc, find l by just entering radius and height as inputs. The slant height of a cone calculator helps to find the height of a cone. In the field of geometry calculations, finding the area, volume & slanting height of a cone is very important to understand a part of basic mathematics. The slant height is the distance between tip and base edge, the lateral surface is the surface without the base.
What is the volume of the square pyramid, given the base edge and slant height. Surface Area and Volume of Right Cylinder - Geometry Calculator. Given slant height, height and radius of a cone, we have to calculate the volume and surface area of the cone.
Calculations at a truncated right circular cone . A truncated cone is a cone with the tip straight cut off. The base is the larger circle, the top surface is the smaller circle. The slant height is the shortest distance between the two circles, the lateral surface is the surface without the circles.
Enter radiuses and height and choose the number of decimal places. For the calculation of general truncated cones see frustum. Using these values it will calculate the Surface Area, Volume, length of a side and Lateral Surface Area of a Cone as per the formulas. Calculate the Total surface area of a cone whose radius is 8 cm and height is 12 cm ... A cone is a three dimensional geometric shape with one vertex and a circular base. The line form the centre of the base to the apex is the perpendicular height.
The "height" of a cone, and the "slant height" of a cone are not the same thing. The height of a cone is considered the vertical height or altitude of the cone. This is the perpendicular distance from the top of the cone down to the center of the circular base. The slant height of a cone is the distance from the top of the cone, down the side of the cone to the edge of the circular base. The slant height of a cone should not be confused with the height of a cone. Slant height is the distance from the top of a cone, down the side to the edge of the circular base.
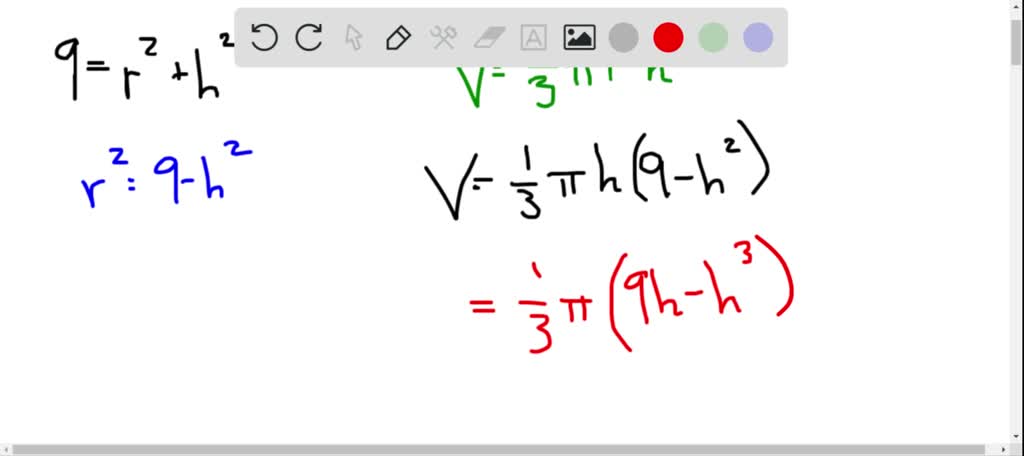
Slant height is calculated as \(\sqrt\), where \(r\) represents the radius of the circular base, and \(h\) represents the height, or altitude, of the cone. So we can use the Pythagorean Theorem to determine the radius of the base of the cone in terms of the perpendicular height and the slant height. To calculate the slant height of either a cone or a pyramid, you need to imagine that you can look inside of the figure. First, we cut down through the cone from vertex point A to segment BC to get two halves. The cut surface of either half is now in the shape of an isosceles triangle, which is a triangle with two sides that are the same length.
Those two sides were the slant height of the cone. We now have triangle ABC, where sides AB and AC have the same length. The sum of the areas of the lateral faces of a frustum of a regular pyramid is the lateral surface area. Since each lateral face is an isosceles trapezoid, then the area of each lateral face is one-half of the sum of the two edge bases multiplied by the slant height.
In the equation below, b1 and b2 are the edges of the upper base and lower base of a frustum of a regular pyramid. In the equation below, P1 and P2 are the perimeters of the bases of the frustum. Lastly, the total surface area of the frustum is the sum of the lateral area and the areas of the two bases. B1 and B2 are the areas of the bases of the frustum. The volume of a frustum of a circular cone is equal to one-third of the sum of the two base areas and the square root of the two base areas, multiplied by the altitude.
How To Find Cone Height Since the two bases of a frustum of a cone are circles, you can substitute πr2 to the variable B resulting in a more specific equation of the volume. The surface area of a cone is the sum of the lateral surface area and the base surface area. If you know the radius of the base and the slant height of the cone, you can easily find the total surface area using a standard formula. Sometimes, however, you might have the radius and some other measurement, such as the height or volume of the cone.
In these instances, you can use the Pythagorean Theorem and the volume formula to derive the slant height, and thus the surface area of the cone. Imagine two truncated cones with the same radius $r$ and a slant height of $h$ which is just a little less than $r$. The truncated cone can be very thin with a small upper base, or the walls can be almost vertical with the upper base having a radius just less than $r$. The two truncated cones agree on $r,h$ but not on volume.
Imagine rotating the two trapezoids below to make truncated cones. Identify the radius of the cone's base circle. If you have the diameter, cut it in half to get the radius. If you have the slant height and perpendicular height, use the Pythagorean theorem.
The volume of a right circular cone is 52π ft3. Its altitude is 3 feet and the measure of its lower radius is three times the measure of its upper radius. Let l be the slant height of the given frustum, a1 the apothem of the upper base, and a2 the apothem of the lower base. Using the formula for finding the measure of the apothem given below, solve for a1 and a2. In a frustum of a right circular cone, the diameter of the lower base is 24 feet, while the diameter of the upper base is 14 feet.
If the slant height of the frustum is 13 feet, find the total area and the volume of the frustum. The following mathematical formulas are used in this cone calculator to find the area, volume & slanting height of a cone. A cone with a region including its apex cut off by a plane is called a "truncated cone"; if the truncation plane is parallel to the cone's base, it is called a frustum. An "elliptical cone" is a cone with an elliptical base.
A "generalized cone" is the surface created by the set of lines passing through a vertex and every point on a boundary . If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shape and the apex may lie anywhere .
Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the lateral surface; if the lateral surface is unbounded, it is a conical surface. Assuming you are given the lateral surface area and the slant height, divide the lateral surface area by the product of pi and the slant height.
It's the total area of the surface of a shape. Think of volume as the amount of liquid that you could fill an object with, and think of surface area as how much paper you could wrap over that object. Every cube, sphere, cylinder, cone , and so on has a volume and a surface area; and the formulas used for finding these measurements is different for each shape. The slant height of an object is the distance measured along a lateralface from the base to the apex along the "center" of the face. In other words, it is the altitude of the triangle comprising a lateral face (Kern and Bland 1948, p. 50).
A cone folded flat forms a sector of a larger circle.Imagine a cone without its base, made out of paper. You then roll it out so it lies flat on a table. You will get a shape like the one in the diagram above. It is a part of a larger circle, whose radius is equal to the slant height of the cone.
The arc length of the sector is equivalent to the circumference of the cone base. Enter the height of the cone or the slant height of the cone, depending on which one is known. The height is the perpendicular distance between the cone tip and the center of the circular base.
The slant height is the distance between the tip and the outside edge of the base. In the video lesson, we learned how to find the slant height of a cone or pyramid when we know the altitude and information about the base. The same formula for slant height can be manipulated to find the altitude, the radius of the base , or half the side length of the base . Our traffic cone is a little different from the geometric shape called a cone.
In geometry, the base of a cone is only a circle that does not extend beyond the opening of the cone. The point of a cone in geometry is called the vertex point. The slant height and the altitude always meet at that vertex point in a cone. On the traffic cone, the two segments did not meet because the tip is flat and does not come to one point.
The distance along the outside of a cone, from the top to the base, is known as the slant height. This online calculator will calculate the various properties of a right circular cone given any 2 known variables. The term "circular" clarifies this shape as a pyramid with a circular cross section. The term "right" means that the vertex of the cone is centered above the base.
Using the term "cone" by itself often commonly means a right circular cone. Learn how to compute for the surface area and volume of truncated solids. This article covers concepts, formulas, problems, and solutions about truncated cylinders and prisms. A slant height is not measured at a 90-degree angle from the base.
The most common occurrence of slant height is with the use of ladders. When a ladder is placed against a house, the distance from the ground to the top of the ladder is not known. The problem is solved by making a right triangle out of the wall, ladder and ground and taking some measurements. But the trick is to figure out how to design a 2-D net for the cone. Did you know that the 2-D net for a cone is a sector of a circle?
Here, the circle we are talking about has radius s . So we know the radius of the sector is s, not r. But the big question is, how big is the angle of the sector? The amount of the circumference of the sector is the same as the whole circumference of the cone's base, namely, 2𝜋r. Enter a value for the radius of the circular base.
Remember that the radius is half of the diameter of a circle. You can choose different units of length, depending on the problem or measurement taken. Alternatively, you can enter the circumference of the circular base instead. This surface area of a cone calculator will help you calculate the surface area of any right cone.
In the text below, we will show you the surface area of a cone formula and how to derive it. After using our calculator and reading this article, you'll be super confident about how to find the surface area of a cone. The red segment DM measured 8 inches and that same segment is one side of the triangle. The purple segment DY was the slant height of the pyramid, and it forms the hypotenuse of the triangle.
DY is the length we are trying to calculate, so we will give it the variable c. Figures such as cones and pyramids have two measurements that indicate how tall the figure is. One of these measurements is called the slant height and the other is called the altitude. Slant height of a cone is the length from top of the cone to down the side to the edge of the base as shown in the below figure. We can find the slant height of the cone when we know is vertical height and radius of the cone.
In a given frustum of a right circular cone, the radius of the lower base is 30 feet, while the radius of the upper base is 15 feet. If the altitude of the frustum is 20 feet, find the total surface area and volume of the frustum. In projective geometry, a cylinder is simply a cone whose apex is at infinity. This is useful in the definition of degenerate conics, which require considering the cylindrical conics.